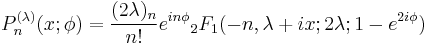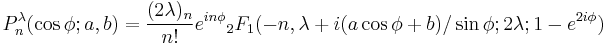Meixner–Pollaczek polynomials

Not to be confused with Meixner polynomials.

In mathematics, the Meixner–Pollaczek polynomials are a family of orthogonal polynomials P(λ)
n(x,φ) introduced by Meixner (1934), which up to elementary changes of variables are the same as the Pollaczek polynomials Pλ
n(x,a,b) rediscovered by Pollaczek (1949) in the case λ=1/2, and later generalized by him.

They are defined by

$P_n^{(\lambda)}(x;\phi) = \frac{(2\lambda)_n}{n!}e^{in\phi}{}_2F_1(-n,\lambda%2Bix;2\lambda;1-e^{2i\phi})$

$P_n^{\lambda}(\cos \phi;a,b) = \frac{(2\lambda)_n}{n!}e^{in\phi}{}_2F_1(-n,\lambda%2Bi(a\cos \phi%2Bb)/\sin \phi;2\lambda;1-e^{2i\phi})$

References

Koekoek, Roelof; Lesky, Peter A.; Swarttouw, René F. (2010), Hypergeometric orthogonal polynomials and their q-analogues, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-642-05014-5, ISBN 978-3-642-05013-8, MR 2656096
Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Pollaczek Polynomials", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248, http://dlmf.nist.gov/18.35
Meixner, J. (1934), "Orthogonale Polynomsysteme Mit Einer Besonderen Gestalt Der Erzeugenden Funktion", J. London Math. Soc. s1-9: 6–13, doi:10.1112/jlms/s1-9.1.6
Pollaczek, Félix (1949), "Sur une généralisation des polynomes de Legendre", Les Comptes rendus de l'Académie des sciences 228: 1363–1365, MR 0030037, http://gallica.bnf.fr/ark:/12148/bpt6k31801/f1363

Meixner–Pollaczek polynomials

See also

References